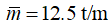Page 83, section “Torsion in beams”
In St. Venant’s torsion, only shear stresses occur as a result of a loading by a torsional moment, but no normal stresses. In the case of cross-sections that are not warp-free, these cause warping of the cross-section. However, no warping occurs as a result of normal stresses.
Page 124, eq. (3.30a)
As for the truss element, the transformed stiffness matrix of the beam can also be given explicitly. For example, a formulation – related to a slightly different local coordinate system – is given in: Falter B., Verallgemeinertes Weggrößenverfahren, in: Schneider Bautabellen für Ingenieure, 24. Auflage, Reguvis Fachmedien GmbH, Köln, 2020, page 4.73
Page 75, References
The following references may be added:
19. Schweda E., W. Krings, Baustatik − Festigkeitslehre, 3. Aufl., Werner Verlag, Düsseldorf, 2000
20. Kraus M., R. Kindmann, Steel Structures: Design using FEM, Ernst&Sohn, Berlin, 2012.
Page 188, references [20] and [35]
Alternatively, the following references can be referred to:
20. Wagner W, Gruttmann F (2002), A displacement method for the analysis of flexural shear stresses in thin-walled isotropic composite beams, Computers & Structures 80, 1843-1851
instead of
20. Wagner W, Gruttmann F (2002), A displacement method for the analysis of flexural shear stresses in thin-walled isotropic composite beams, Universität Karlsruhe, Mitteilungen des Instituts für Baustatik 3, Karlsruhe, 2002
and
35. Wagner W, Sauer R, Gruttmann F (1999), Tafeln der Torsionskenngrößen von Walzprofilen unter Verwendung von FE-Diskretisierungen, Stahlbau 68, Ernst & Sohn, Berlin, 102-111
instead of
35. Wagner W., R. Sauer, F. Gruttmann, Tafeln der Torsionskenngrößen von Walzprofilen unter Verwendung von FE-Diskretisierungen, Universität Karlsruhe, Mitteilungen des Instituts für Baustatik, 5, Karlsruhe
Page 317: 4.10.4 Connections with Stress Assumptions (EST)
In some commercial programs the so-called RBE3 element is implemented. Rather than being a finite element, it is a coupling condition of nodes. The motion of a reference node is defined as the weighted average of the motions of a group of nodes. The reference node corresponds to the beam node of the EST approach, the group of connected nodes corresponds to the nodes of the FE mesh connected to the beam element. As in EST, the determination of the displacements and rotations of the reference node is based on the principle of virtual work. The underlying approach is thus the same as for EST: Instead of specifying the displacement distribution at the coupling area via an MPC condition (and thus defining a rigid inclusion in the FE model), one specifies the stress or force distribution at the coupling area and determines the displacements according to the principle of virtual work. However, for the RBE3 element the weighting factors can be chosen freely by the user. With the appropriate choice of weighting factors (based on the stress distribution of the beam), the RBE3 element will match the EST approach. The RBE3 element is usually applied for the weighted distribution of forces acting at the reference node to several nodes of the FE mesh.
References
NX Nastran 12, Advanced Nonlinear Theory and Modeling Guide”, Siemens Procuct Lifecycle Management, 2017, pages 111-115
Sandia Report, SAND2017-11104, Sierra/SD-Theory Manual, Sandia National Laboratories, Albuquerque/New Mexica and Livermore/Calífornia, USA, 2017, pages 167-174
Pages 631, 632, eqns. 588a, 588b
Shear waves and compressional waves are also denoted as S-waves and P-waves, respectively.
Page 637, Example 5.22
For consistency with Table 5.9 the distributed mass m should be written with an overbar in: